人間の見える感覚を数値化するのはほぼ不可能に近いと思われるが、以下はその試みのひとつである。

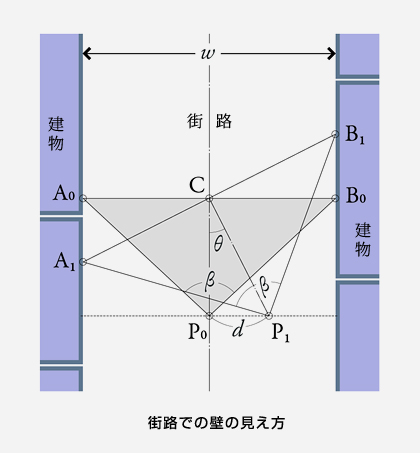
右図は街路を上空から俯瞰したすがたを表現している。街路の中央P₀に存在する人間の視線が両側の建物の外壁を等しく射る地点をA₀とB₀とする。このときA₀P₀とB₀P₀がなす角度βは人間の視界とも注意力の働く範囲とも捉えられる。

ここで街路の幅員方向にP₀からP₁に移動すると、先程の△A₀B₀P₀は△A₁B₁P₁に変化し、ふたつの三角形はCで交わる頂角βの互いに相似な二等辺三角形である。

A₀の見え方を［A₀］で表現すると［A₀］＋［B₀］がP₀での見え方を表現しているから、任意の地点P_nでの［A_n］＋［B_n］を式で表せば見え方の変化を調べることができる。

建物の壁面の見え方はふたつの要素の積によって表現される。要素のひとつは距離の変化による縮小率、要素のふたつめは壁面を斜めから見ることによる水平方向の縮小率、前者は二次元的、後者は一次元的に作用する。

P₀からの移動を角度θで表現すると

（距離の変化による縮小率）＝cos²θ
（壁面を斜めから見ることによる水平方向の縮小率）＝cos(∠R−β/2＋θ)＋cos(∠R−β/2−θ)

したがって壁の見え方yは以下の式で示され、これをグラフ化すれば壁の見え方の変化の様子を図示できる。

y＝cos²θ{cos(∠R−β/2＋θ)＋cos(∠R−β/2−θ)}
ただし−β/2≦θ≦β/2

いまθの変化を街路中心P₀からの移動の距離dの変化で表現し、その変化量xを半幅員に対する割合で定義する。
すなわちx＝d÷w/2とする。このとき壁の見え方yは以下の式で示される

《β＝90°の場合》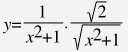
《β＝120°の場合》

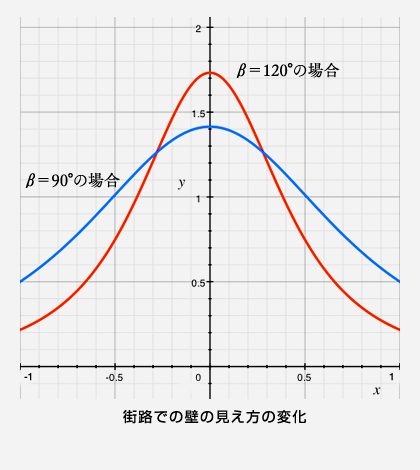
上の式をMacのGrapherでグラフ化したものが右図であり、青が《β＝90°の場合》、赤が《β＝120°の場合》の壁の見え方の変化の様子を示めしている。

x軸の0が街路中央、1と-1は街路端を意味しており、位置の違いによる壁の見え方の変化がきれいに表現されている。